00. Quick Start

Imports

the fdtd library is simply imported as follows:

import fdtd

Setting the backend

the fdtd library allows for setting a backend. There exist a Numpy backend and several PyTorch backends. The available backends are: - "numpy" (defaults to float64 arrays) - "torch" (defaults to float64 tensors) - "torch.float32" - "torch.float64" - "torch.cuda" (defaults to float64 tensors) - "torch.cuda.float32" - "torch.cuda.float64"

In general, the "numpy" backend is preferred for standard CPU calculations with "float64" precision. In general, "float64" precision is always preferred for FDTD simulations, however, "float32" might give a significant performance boost.

The "cuda" backends are only available for computers with a GPU.

fdtd.set_backend("numpy")

The FDTD-grid

The FDTD grid defines the simulation region.

# signature
fdtd.Grid(
    shape: Tuple[Number, Number, Number],
    grid_spacing: float = 155e-9,
    permittivity: float = 1.0,
    permeability: float = 1.0,
    courant_number: float = None,
)

A grid is defined by its shape, which is just a 3D tuple of Number-types (integers or floats). If the shape is given in floats, it denotes the width, height and length of the grid in meters. If the shape is given in integers, it denotes the width, height and length of the grid in terms of the grid_spacing. Internally, these numbers will be translated to three integers: grid.Nx, grid.Ny and grid.Nz.

A grid_spacing can be given. For stability reasons, it is recommended to choose a grid spacing that is at least 10 times smaller than the smallest wavelength in the grid. This means that for a grid containing a source with wavelength 1550nm and a material with refractive index of 3.1, the recommended minimum grid_spacing turns out to be 50nm

For the permittivity and permeability floats or arrays with the following shapes

• (grid.Nx, grid.Ny, grid.Nz)

• or (grid.Nx, grid.Ny, grid.Nz, 1)

• or (grid.Nx, grid.Ny, grid.Nz, 3)

are expected. In the last case, the shape implies the possibility for different permittivity for each of the major axes (so-called uniaxial or biaxial materials). Internally, these variables will be converted (for performance reasons) to their inverses grid.inverse_permittivity array and a grid.inverse_permeability array of shape (grid.Nx, grid.Ny, grid.Nz, 3). It is possible to change those arrays after making the grid.

Finally, the courant_number of the grid determines the relation between the time_step of the simulation and the grid_spacing of the grid. If not given, it is chosen to be the maximum number allowed by the Courant-Friedrichs-Lewy Condition: 1 for 1D simulations, 1/√2 for 2D simulations and 1/√3 for 3D simulations (the dimensionality will be derived by the shape of the grid). For stability reasons, it is recommended not to change this value.

grid = fdtd.Grid(
    shape = (25e-6, 15e-6, 1), # 25um x 15um x 1 (grid_spacing) --> 2D FDTD
)

print(grid)

Grid(shape=(161,97,1), grid_spacing=1.55e-07, courant_number=0.70)

Adding an object to the grid

An other option to locally change the permittivity or permeability in the grid is to add an Object to the grid.

# signature
fdtd.Object(
    permittivity: Tensorlike,
    name: str = None
)

An object defines a part of the grid with modified update equations, allowing to introduce for example absorbing materials or biaxial materials for which mixing between the axes are present through Pockels coefficients or many more. In this case we’ll make an object with a different permittivity than the grid it is in.

Just like for the grid, the Object expects a permittivity to be a floats or an array of the following possible shapes

• (obj.Nx, obj.Ny, obj.Nz)

• or (obj.Nx, obj.Ny, obj.Nz, 1)

• or (obj.Nx, obj.Ny, obj.Nz, 3)

Note that the values obj.Nx, obj.Ny and obj.Nz are not given to the object constructor. They are in stead derived from its placing in the grid:

grid[11:32, 30:84, 0] = fdtd.Object(permittivity=1.7**2, name="object")

Several things happen here. First of all, the object is given the space [11:32, 30:84, 0] in the grid. Because it is given this space, the object’s Nx, Ny and Nz are automatically set. Furthermore, by supplying a name to the object, this name will become available in the grid:

print(grid.object)

    Object(name='object')
        @ x=11:32, y=30:84, z=0:1

We can add a second object to the grid:

grid[13e-6:18e-6, 5e-6:8e-6, 0] = fdtd.Object(permittivity=1.5**2)

Here we chose to slice the grid with floating point numbers, which will be replaced by integer Nx, Ny and Nz during the registration of the object. Since we didnt give the object a name, the object won’t be available to us as an attribute of the grid. However, it is still available to us via the grid.objects list:

print(grid.objects)

[Object(name='object'), Object(name=None)]

This list stores all objects (i.e. of type fdtd.Object) in the order that they were added to the grid.

Adding a source to the grid

Similarly as to adding an object to the grid, an fdtd.LineSource can also be added:

# signature
fdtd.LineSource(
    period: Number = 15, # timesteps or seconds
    amplitude: float = 1.0,
    phase_shift: float = 0.0,
    name: str = None,
)

Similarly to an fdtd.Object, an fdtd.Source size is defined by its placement on the grid:

grid[7.5e-6:8.0e-6, 11.8e-6:13.0e-6, 0] = fdtd.LineSource(
    period = 1550e-9 / (3e8), name="source"
)

However, it is important to note that in this case we are adding a LineSource, i.e. the source spans the diagonal of the cube defined by the slices. Internally, these slices will be converted into lists to ensure the expected behavior:

print(grid.source)

    LineSource(period=14, amplitude=1.0, phase_shift=0.0, name='source')
        @ x=[48, ... , 51], y=[76, ... , 83], z=[0, ... , 0]

Note that one could have also supplied lists to index the grid in the first place. This feature could be useful to create a LineSource of arbitrary shape.

Adding a detector to the grid

Adding a detector to the grid works the same as adding a source

# signature
fdtd.LineDetector(
    name=None
)

grid[12e-6, :, 0] = fdtd.LineDetector(name="detector")

print(grid.detector)

    LineDetector(name='detector')
        @ x=[77, ... , 77], y=[0, ... , 96], z=[0, ... , 0]

Adding grid boundaries

Although, having an object, source and detector to simulate is in principle enough to perform an FDTD simulation, One also needs to define a grid boundary to prevent the fields to be reflected. One of those boundaries that can be added to the grid is a Perfectly Matched Layer or PML. These are basically absorbing boundaries.

fdtd.PML(
    a: float = 1e-8, # stability factor
    name: str = None
)

# x boundaries
# grid[0, :, :] = fdtd.PeriodicBoundary(name="xbounds")
grid[0:10, :, :] = fdtd.PML(name="pml_xlow")
grid[-10:, :, :] = fdtd.PML(name="pml_xhigh")

# y boundaries
# grid[:, 0, :] = fdtd.PeriodicBoundary(name="ybounds")
grid[:, 0:10, :] = fdtd.PML(name="pml_ylow")
grid[:, -10:, :] = fdtd.PML(name="pml_yhigh")

Grid summary

A simple summary of the grid can be shown by printing out the grid:

print(grid)

Grid(shape=(161,97,1), grid_spacing=1.55e-07, courant_number=0.70)

sources:
    LineSource(period=14, amplitude=1.0, phase_shift=0.0, name='source')
        @ x=[48, ... , 51], y=[76, ... , 83], z=[0, ... , 0]

detectors:
    LineDetector(name='detector')
        @ x=[77, ... , 77], y=[0, ... , 96], z=[0, ... , 0]

boundaries:
    PML(name='pml_xlow')
        @ x=0:10, y=:, z=:
    PML(name='pml_xhigh')
        @ x=-10:, y=:, z=:
    PML(name='pml_ylow')
        @ x=:, y=0:10, z=:
    PML(name='pml_yhigh')
        @ x=:, y=-10:, z=:

objects:
    Object(name='object')
        @ x=11:32, y=30:84, z=0:1
    Object(name=None)
        @ x=84:116, y=32:52, z=0:1

Running a simulation

Running a simulation is as simple as using the grid.run method.

grid.run(
    total_time: Number,
    progress_bar: bool = True
)

Just like for the the lengths in the grid, the total_time of the simulation can be specified as an integer (number of time_steps) or as a float (in seconds).

grid.run(total_time=100)

100%|██████████| 100/100 [00:00<00:00, 532.90it/s]

Grid visualization

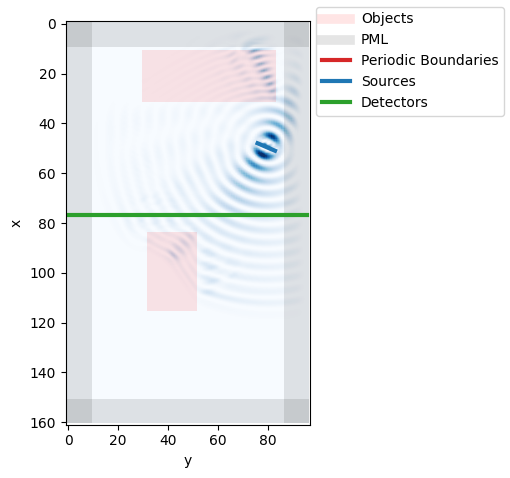
Let’s visualize the grid. This can be done with the grid.visualize method:

# signature
grid.visualize(
    grid,
    x=None,
    y=None,
    z=None,
    cmap="Blues",
    pbcolor="C3",
    pmlcolor=(0, 0, 0, 0.1),
    objcolor=(1, 0, 0, 0.1),
    srccolor="C0",
    detcolor="C2",
    show=True,
)

This method will by default visualize all objects in the grid, as well as the current field intensity at a certain x, y OR z-plane. By setting show=False, one can disable the immediate visualization of matplotlib.

grid.visualize(z=0, show=False)
import matplotlib.pyplot as plt